On gaining access to a diverse range of additional chemicals, the brothers decided to formulate some products that they would be able to bottle, brand and sell. Consequentially, they proceeded to develop a range of specialised automotive products, which included products such as rust removing and inhibiting gels, additives that modified the electrolyte of the lead acid battery to optimise performance and extend life, various types of siliconised protective polishes and coatings, oil additives, cavity sealants, etc. etc. They then diversified their activities into the development and manufacture of several unique performance and economy enhancing products such as steam, and water injection units, transistorised electronic ignition systems, etc. The branded retail products were marketed via a separate mail order company and through a network of authorised agents.

In the early 1990’s, after having worked tirelessly since the inception of the business and having withstood the economic recession that occurred in the 1980’s, and in view of the fact that both of their grandfathers had not lived to see 70, and their father had died at the relatively young age of 58, the brothers decided to take early retirement and live a more leisurely life. Keith’s brother promptly emigrated to Surfers Paradise in Queensland, Australia in order to realise one of his childhood dreams, and Keith was able to travel the world and spend more time at his holiday home in Malta. Having, once again, turned his attention to various scientific matters, Keith embarked on an aeronautical project and, with the help of his son, manufactured and successfully flew a model of a revolutionary vertical take off and landing machine that he had designed and developed over the course of several years. The machine, which resembles the classic depiction of what can only be described as a flying saucer, is entirely unique and, unlike the fragile, twitchy helicopter, it is much more robust and has a service ceiling that rivals that of any fixed wing aircraft.

Rather than gullibly swallow an unproven mathematical theory that can be likened to some baseless myth that sustains an irrational belief, Keith instinctively adopts the objective viewpoint advocated by the famous French philosopher and mathematician René Descartes (1596-1650) who prudently stated: “If you would be a real seeker after truth, it is necessary that at least once in your life you doubt, as far as possible, all things.” Moreover, Keith has long been aware of the fact that many eminent experimental physicists who were the contemporaries of Albert Einstein, such as the inventor of the atomic clock, Louis Essen, the astrophysicist Herbert Dingle, plus the distinguished Nobel Laureates J. J. Thomson, Ernest Rutherford, Albert Michelson, Frederick Soddy, Hannes Alfvén, et al, steadfastly refused to accept the relativity theories that were proposed by Einstein and repeatedly alleged that the underlying principles are not grounded in physical reality. Therefore, after having thoroughly researched the subject from a practical viewpoint and having received much encouragement from friends and family, Keith eventually put pen to paper and wrote a comprehensive and comprehensible book in which he contends that as per the legitimate reservations of a significant number of qualified experimental physicists, Einstein’s theories are fundamentally flawed because, primarily, Einstein was a mathematician, not an experimental physicist; thus, as he lacked practical experience, he only conducted elaborate thought experiments in order to test his innovative theories without taking account of the fact that, in reality, thought experiments are essentially thoughts without experiments.

As Keith knows only too well, unless you perform practical experiments to rigorously test what seems like a good idea, you’ll never know for certain whether the idea is any good. Accordingly, referring to his past experiences in chemical engineering and product development, he says that whenever he embarked on the development of a new product he always commenced by writing the sales literature that he intended to use to promote the finished product. Therefore, he would detail the performance of the intended product and list all the benefits that he hoped would ensue as a consequence of using it. Hence, he may have written something such as: “Not only does the product do A, B and C, but it also enables you to eliminate D, E and F without needing to waste valuable time and money applying a conventional X.” Although the formulation of the product might have been technically feasible, he was always aware of the fact that the preliminary sales leaflet was only a provisional description of the intended product; in other words, it was equivalent to a scientific theory that needed testing because the product had not at that stage been manufactured. Therefore, the harsh reality meted out by the inflexible laws of nature would determine the product’s fate; thus, if it couldn’t be made, or didn’t perform, then the notional product would not survive.

However, as Keith frequently points out, theoretical physicists, unlike experimental physicists, are not constrained by rational laws of nature when they deftly exploit tricks of pure mathematics in order to fashion an exquisitely tailored cloak of algebraic respectability for their pet theory. This is because all traces of the debatable line that used to separate arithmetical speculation from logical fact-based theorising have now been erased. Consequently, the only tests that most contemporary theories need to pass prior to them being accepted by the scientific establishment are those conducted by mathematicians. In effect, the distinction between physics and mathematics, or, more to the point, between a reality-based scientific theory and a thought-based philosophy, has been blurred. Einstein once referred to this unsatisfactory state of affairs, which to a large extent he had been responsible for, when he astutely observed: “The physicists say that I am a mathematician, and the mathematicians say that I am a physicist. I am a completely isolated man and though everybody knows me, there are very few people who really know me.”

Therefore, as Keith rationally argues, it’s hardly surprising that as a consequence of pursuing an abstract mathematical route, ambitious theoreticians often throw caution to the wind and insist that because their contrived mathematical evidence is sound, their embryonic theories must be valid. Moreover, instead of conceding that a new theory is fatally flawed owing to the fact that the basic hypothesis upon which it has been based could easily be falsified because it is reliant on implausible unrelated suppositions that result in obvious contradictions, modern theorists have a tendency to assertively argue that some ad hoc set of complex mathematical equations, which they have resourcefully originated by means of intuition and guile, equates to a critical mass of compelling evidence that authenticates an array of unproven assertions. Additionally, whenever their theoretical contentions are subjected to rigorous scrutiny by cautious doubters and found wanting, theorists expediently fill any embarrassing gaps that the perceptive critics might have identified in a provisional version of the theory by arbitrarily modifying their ingenious equations. Consider, for example, the widely acclaimed ‘superstring theory’, which Keith, along with many distinguished scientists who are actively engaged in applied physics, justifiably alleges has been responsible for luring an entire generation of the brightest mathematicians-cum-theoreticians down an intellectual blind alley.

Indisputably, it is clear from all available evidence that countless creative young minds have been encouraged to participate in the development of what is often described by experimental physicists as an incomplete, scientifically useless, highly speculative theory. Yet, despite the defensible criticism, many of today’s leading theoreticians, who have been directly influenced by Albert Einstein, stubbornly argue that the ingenious unfinished string theory is much too elegant to be wrong. Furthermore, those who belong to the string cognoscenti habitually attempt to justify some of the wilder unsubstantiated elements of the theory by drawing attention to the fact that Einstein once boldly stated: “If at first, the idea is not absurd, then there is no hope for it.” Although these enthused theorists revere the mathematical exploits of Einstein and share his views about the inherent power and absolute truth of pure mathematics, the material facts don’t corroborate their shared optimism, which is more akin to the evangelical fervour that one associates with a religious bigot than the reasoned judgement of a sober logician. Consequentially, to the detriment of the ongoing struggle to improve the quality of human knowledge, string theory, like Einstein’s relativity theories, now predominates theoretical physics, and, due to its dominance, any physicist who is bold enough to highlight intrinsic inconsistencies or proffer an alternative theory is unjustly regarded as a dissident. This invariably results in innocent critics being ostracised from the mainstream by their brainwashed blinkered peers.

Does Science need Mathematical Beauty and Obscure Poetic Hype?

“Beauty is truth, truth beauty,” ... that is all
Ye know on earth, and all ye need to know.

The enigmatic concluding lines of ‘Ode on a Grecian Urn’ written by John Keats (1795-1821)

Having loosened their psychological grip on objective reality, many mathematicians and theoretical physicists irrationally echo the sentiments of the English poet John Keats when they attribute beauty to mathematical proofs, and refer to the elegance of algebraic equations that shore up unconventional abstract theories. Yet, it is patently obvious that to insist that a theory must be true simply because it is deemed to be beautiful is a glaring admission that the underlying principles have been rooted in unfounded conjecture that cannot hold sway on its own merits. Nonetheless, when Einstein discussed the four-dimensional mathematical manifold that underpins his general theory of relativity with the illustrious German philosopher of science Hans Reichenbach, he informed him that he had always known that his theory must be true because it was so beautiful. Similarly, much like modern-day string theory, the failed vortex theory of atoms that was advanced by Lord Kelvin in 1867, and which gained the support of many eminent theorists including the famous James Clerk Maxwell, was once described as being far too beautiful not to be true. Kelvin had been inspired by the stability and vibrational properties of smoke rings and had suggested that atoms are probably minute toroidal whirlpools in some homogeneous, incompressible, frictionless ether that pervades the universe. The distinctive physical and chemical properties of the atoms of each of the elements were believed to be governed by the disparate geometrical shapes and vibrations of the vortices. However, beautiful proofs can be false, and elegant equations and theories can be flawed as was Kelvin’s theory of autogenic vortically gyrating ring-shaped atoms. Prior to vortex theory’s demise, theoreticians, awed by its innate complexity, had been of the same mindset of modern-day string theorists and had predicted that it would take several generations to fully develop the theory’s rudimentary mathematical foundations.

Taking account of the aforementioned facts, the ongoing development of string theory can be likened to a sophisticated mathematical exercise that perpetuates a mental battle that theorists are waging to salvage a theory which, thus far, has failed to provide a convincing explanation for the relationship that allegedly exists between the disparate forces of nature and the baryonic matter that manifests itself in the material existence of the universe. Moreover, because most of its predictions are untestable, the beautiful string theory is considered to be outside the purview of accepted science by the majority of experimental physicists and a sizeable number of dispirited theoreticians. What is even more alarming, the dissenters allege that the state of modern physics is the tragic consequence of an obsolete belief system that is reliant on conceptual mathematics, and the critical comments that follow serve to legitimise their argument: "I don't like that they're not calculating anything. I don't like that they don't check their ideas. I don't like that anything that disagrees with experiment they cook up an explanation; a fix-up all the time to say, 'well it still might be true'." Those words were uttered by the distinguished theorist and Nobel Laureate Richard Feynman (1918-1988) over 20 years ago when he authoritatively described string theory as theoretical nonsense and angrily added: “String theorists don’t make predictions, they make excuses!” In a similar vein, the belated admissions of some disillusioned theorists such as Lee Smolin, Peter Woit, Daniel Friedmen, plus the Nobel Laureates Philip Anderson, Sheldon Glashow, David Gross, and Robert Laughlin, all of whom have devoted their working lives to the advancement of physics and in many instances have participated in the development of string theory, and who allege that progress has been impeded as we have made no real headway in theoretical physics during the past 40 years, vindicate the opinions of many doubters who, like Feynman, have come to realise that enthusiastic myopic promoters of abstract mathematical theories should wake up, embrace reality and stop trying to pass off what amounts to little more than beguiling science fiction as some arcane geometrical model of physical reality.

Briefly, the relevant facts are that string theory, allegedly at the cutting edge of theoretical physics, is habitually depicted as an ambitious attempt to mathematically model the behaviour of the fundamental constituents of the universe. The trouble is that the majority of physicists know that the theory, which originated way back in 1968 during an attempt to understand the strong force that is alleged to bind the protons and neutrons together within the nucleus of an atom, has been going nowhere fast for the past 40 years. The initial intranuclear version failed dismally because it predicted sub-nucleonic string-like particles of a type that had zero mass. Rather than dump the theory in the failed-ideas trash can where it undoubtedly belongs, desperate theorists decided that it needed to be reinterpreted, not as the theory of nuclear force, but as a theory that would unify all forces, including gravity. The unwelcome particles of zero mass could now be identified with the hypothetical quanta of gravitational radiation, the so-called "gravitons".

In order to effect the desired transition from a theory of subatomic force to the theory of everything, when the notional strings were liberated from the nucleus of the atom their size was reduced by a factor of twenty to make them conform to the Planck length. This ruled out any possibility of verifying the theory experimentally because the Planck length to the size of an atom is equivalent to the size of an atom compared to the size of the Solar System. Another amusing difficulty was that the theory required that the ubiquitous space-time should comprise of 26 dimensions. Dedicated string theorists doggedly soldiered on and eventually reduced the requisite number of dimensions to 10, and then resorting to microgeometry they employed an abstract mathematical process called "compactification" to wrap up 6 of the dimensions and cause them to become tiny tightly furled spheres so that, effectively, the minute curled up entities are rendered all but invisible and thus the 3 orthogonal dimensions and 1 of time remain virtually unchanged. When the leading proponent of string theory, Edward Witten (1951- ), who is often referred to as Einstein’s successor, was asked to explain why he thought three dimensions of space should be larger than six additional spatial co-ordinates, he was unable to provide a satisfactory or sensible answer and simply stated: “That’s a big problem that has to be explained. As of now, string theorists have no explanation of why there are three large dimensions as well as time, and the other dimensions are microscopic. Proposals about that have been all over the map.” Clearly, it is evident from Witten’s answer that string theorists are unable to distinguish spatial dimensions, which are essentially abstract, useful and necessary geometrically configured aspects of measurement, from material components of physical reality.

Nevertheless, ignoring the confusion that arises due to the insubstantiality of spatial dimensions, and despite the numerous arbitrary adjustments that were made to string theory, the Mark 2 version still had a fatal flaw as it predicted particles of imaginary mass due to their notional energy content being expressed as a multiple of the square root of minus one. As a consequence of their negative imaginary mass, the particles were presumed to travel faster than the speed of light, and thus travel backwards through time. The unphysical characteristics and behaviour of the superluminal particles, which were eventually dubbed "tachyons", gave rise to the hypothetical existence of a bizarre device, which inventive theorists referred to as a “tachyonic antitelephone”, that was capable of transmitting eerie signals and messages into the dim and distant past. Not surprisingly, the embarrassing tachyon conundrum duly brought string theory to its knees as many physicists gave up the subject in disgust believing that such exotic particles can't exist.

Yet again, new life was breathed into the crumbling theory with the introduction of the mathematical concept of supersymmetry. This ploy eliminated the tachyons and thereby made the theory appear more consistent, and because the infinitesimal supersymmetric strings of energy, depending on their frequency of vibration, could now manifest themselves as either fermions, fundamental particles of matter, or bosons, the hypothetical particles that convey the forces of nature, a unified superstring theory Mark 3 was born. Theorists began to glibly talk about a parameter which they termed “alpha prime”. Alpha prime is supposed to quantify the tension of each of the non-material strings, which, fundamentally, are supposed to be identical in that each string consists of either an open strand or a minuscule string-like loop of pure energy depending on which version of the theory you choose to support. What the primordial pure energy looked like, how it was created, from what source it originated, and why it became separated into a countless number of discrete entities are pertinent questions that string theorists shy away from because they are unable to invent plausible answers. Nonetheless, they confidently assert that different harmonics that result from the constantly quivering strings of energy now correspond to different elementary particles as per the unrealised dream of Einstein who had believed that matter and forces are ultimately manifestations of complex geometrical forms that collectively equate to some idealised representation of the four-dimensional fabric of space-time.

As per usual, despite many imaginative modifications, there were still unresolved problems in the supersymmetric version of string theory due to the appearance of mathematical inconsistencies, which are referred to as "anomalies". Undaunted by the technical difficulties, artful mathematicians diligently persevered and proceeded to derive anomaly cancellations to placate the critics. Notwithstanding their ingenious mathematical tricks, the modified equations still threw up infinities in the middle of calculations that are meaningless for physical purposes because performing such calculations is equivalent to dividing 1 by zero. What is more, we now learn from dissident string theorists that the theory is unable to cope with the claim that 73% of the cosmos is comprised of the mysterious antigravity force that is referred to as "dark energy". The divergence between theoretical prediction and practical observations prompted the eminent theorist Sheldon Glashow, who gained a Nobel prize for his work on the theory of the electroweak intranuclear force that manifests itself in beta decay, the emission of electrons or positrons by neutrons in radioactive atomic nuclei, to criticise string theory for being entirely mathematical, thus devoid of any experimental proof, and to disparagingly label it as a “new version of medieval theology.” Moreover, when theoreticians threw a lavish party to celebrate the 20th anniversary of superstring theory, referring to the generally accepted appraisal of Einstein’s marathon fruitless attempt to construct a mathematical theory of everything that would unify the forces of nature with material constituents of the universe, Glashow poured scorn on the gleeful gathering with the withering observation: “So when one person spends 30 years, it’s a waste, but when thousands waste 20 years in modern day, they celebrate with champagne. I find that curious.”

In reality, because its experimental pedigree amounts to nothing more than wishful thinking, string theory can legitimately be regarded as a baseless mathematical hunch. Furthermore, unlike a logical testable scientific explanation for natural phenomena, it will never, according to the lapsed string theorist Lee Smolin, be able to be falsified experimentally due to the fact that, currently, there are approximately 10 to the power of 500 variants of the theory in existence. Therefore, no conceivable experiment could ever disagree with all of the disparate versions. As a consequence of the prevailing state of uncertainty, the eminent string theorist David Gross was moved to state: “We don’t know what we are talking about!” He then admitted: “Many of us believed that string theory was a very dramatic break with our previous notions of quantum theory. But now we learn that string theory, well, is not that much of a break.” Gross concluded his revelatory address with the assertion that theoretical physics is now in “a period of utter confusion.” Similarly, the eminent particle physicist Peter Woit complained: “Too many people have been overselling a very speculative idea... String theory has produced nothing.”

Considering the fact that string theory is a theory that is supposed to explain everything, it’s somewhat disturbing to discover that there are thousands of versions of the theory under construction that permit the existence of innumerable parallel universes, and that a former top string theorist, Daniel Friedman, has scathingly declared that “string theory is a complete scientific failure.” However, it comes as no surprise to learn that one of the latest jokes about the theory is that we can, after all, say that our universe is unique. Why? Because it is the only one that string theory cannot describe. Although narrow-minded devotees of string theory might accuse the aforementioned dissenters and their fellow sceptics of being gamekeepers who have turned poachers, they would be wiser to err on the side of caution and uphold the right to the freedom of speech by commending their objective critiques because, surely, science can only benefit from such frank appraisals; whereas, a complacent string theorist stands to lose nothing other than a prejudiced untestable opinion that subsists on blind belief. As Richard Feynman eloquently stated when he cautioned theorists with a mathematical bent to heed the results of practical experiments: “It doesn’t matter how beautiful your theory is, it doesn’t matter how smart you are. If it doesn’t agree with experiment, it’s wrong.” Had Einstein, the archetypal insular theorist, taken the trouble to familiarise himself with results of practical experiments instead of relying on the infallibility of intuitive mathematical prediction, he would, in all probability, not have eagerly derived the following discredited theory of flight that resulted in his little-known futile attempt to improve the performance of an aircraft’s wing.

Einstein’s Monumental Aeronautical Blunder

As a consequence of having conducted much research into the science of fluid mechanics, which requires consideration of Reynolds numbers that indicate the quality of laminar flow, various effects that pertain to boundary layer control, plus knowledge of the Coanda effect, Magnus effect, and vortex shedding, etc., and which is key to understanding and improving the performance of heavier-than-air flying machines, the author of 'What Einstein Didn't Know About Time' is surprised that the general public are never made aware of the fact that in 1916, during the First World War, Einstein published a technical paper on the phenomenon of flight, which, as every physicist who has studied the paper knows, is a work of fanciful fiction. Einstein goofed for the simple reason that, like everybody else, he wasn’t superhuman. He authoritatively concocted an erroneous theory, his theory was subjected to the ultimate test and it failed. Moreover, not only did Einstein fail in his attempt to enhance the performance of a wing, but his folly almost resulted in the deaths of two competent test pilots.

You can read an account of Einstein’s foray into the science of flight in the following brief out-take that failed to make the final edit in Keith Ashworth’s controversial book that shatters the myth of relative time.

During the First World War when Einstein was based at Berlin University and allegedly at the peak of his mental powers, the German aircraft manufacturer Luft-Verkehrs-Gesellschaft hired him as a consultant to advise on modifications that might improve the performance of their aeroplanes. Turning his attention to the science of aerodynamics, Einstein decided to design an improved wing that would generate more lift. On 16 August 1916, after having resorted to mathematics while attempting to devise a tenable theory of flight, Einstein published a technical paper on the project that began with the intriguing question: “Where does lift come from that allows airplanes and birds to fly?” Referring to the famous equation derived in the eighteenth century by the Swiss mathematician Daniel Bernoulli (1700-1782) that states that as the velocity of a fluid increases, the increase in speed causes the pressure of the moving fluid to decrease, he attempted to answer his own question and proceeded to cite what many aeronautical engineers refer to as the “equal transit time fallacy”, which is based on the widely held yet mistaken belief that the particles of air that are forced to separate from eac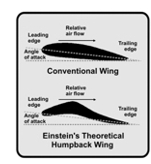h other at the leading edge of a wing in order to flow above or beneath the aerofoil must rejoin at the rear trailing edge. In essence, Einstein assumed that provided the upper surface of an aerofoil is curved causing the distance travelled by the particles of air to be longer than the distance traversed by those flowing below, then the relative speed of the uppermost airstream will be higher and thus the air pressure will be lower as a consequence of the camber on the topside of the wing. Convinced that the flaky theory was sound, Einstein revealed his innovative design that featured an enormous hump strategically placed on the upper surface of the wing, and, fuelled with enthusiasm, he proudly advanced a speculative calculation that quantified the additional lift that the cumbersome hump would theoretically produce due to the longer path that the air would be forced to travel.

A section of the experimental wing, which, due to its distinctive arched profile, was dubbed the “cat’s back aerofoil”, was then tested in a wind tunnel in Gottingen. Although the results were disappointing and revealed that the lift-to-drag ratio was extremely poor, the manager of the aircraft factory, which was located in Berlin, Paul Georg Ehrhardt, decided to go ahead and test the strange new wings. Einstein’s wings were duly manufactured and fitted to a World War One biplane; an LVG (D9V) C.II. After an exceedingly long take-off run, the modified plane reluctantly struggled into the air and immediately went into an uncontrollable roll. Ehrhardt later said that he was extremely fortunate in that he managed to land the plane quickly and safely, and added: “I was overjoyed to find myself on firm ground and still in one piece.” Apparently, the aeroplane had been extremely difficult to control because Ehrhardt reported that it had had a tendency to “waddle while flying something akin to the flight of a pregnant duck.” A second test pilot, Otto Reichert, experienced a similar lucky escape when his plane suffered engine failure due to the excess drag. He then clipped a power line while attempting to make a dead stick landing, which caused his plane to crash and burst into flames. Both test pilots stated that they only felt safe when flying the modified plane straight and level close to the ground at the airfield as it was not stable enough to perform routine manoeuvres and turns. Therefore, instead of generating additional lift, Einstein’s novel wings had the opposite effect and gave a functional aircraft unusual and dangerous flight characteristics.

Einstein was forced to accept the fact that his revolutionary wing design had been a disastrous failure. However, when he subsequently wrote to Ehrhardt, he resorted to humour in an attempt to make light of the embarrassing episode and apologetically explained: “That is what can happen to a man who thinks a lot, but reads little.” The revealing incident obviously continued to haunt him thereafter because in 1954, one year prior to his demise, after having admitted that his contribution to aerofoil design had been “folly”, Einstein, once again, attempted to justify his erroneous over-simplified train of thought when he wrote: “Although it is probably true that the principle of flight can be most simply explained in this [Bernoullian] way, it by no means is wise to construct a wing in such a manner!” Clearly, he had not been aware of the fact that the more cautious Bernoulli would not have endorsed his idealised mathematical theory of flight as he had rationally argued: "It would be better for true physics if there were no mathematicians on Earth."

What Einstein had negligently failed to realise is that whenever air flows over, and thus relative to the positive curve on the upper surface of a wing, the relative flow of the air is initially caused to slow down and move in an upward direction, and the change in direction involves acceleration and force. The force that results from the reaction pushes the wing down. The moment the air clears the crest of the curve it is deflected down due to the Coanda effect, which strives to prevent a vacuum forming. Although the deflected air is then caused to accelerate relative to the wing, the wing reacts and is caused to accelerate with respect to the air, and the upward accelerated motion of the wing, which is referred to as “lift”, is assisted by the increased pressure of the air flowing beneath the underside of the wing. Therefore, it is imperative that a theoretician does not lose sight of the fact that if the air flowing over the top of a wing has a uniform speed and an equal transit time to that of the air flowing below, then, regardless of the profile of the wing, the air might just as well be still as nothing will ever change; hence, there will be no dynamic circulation, no forces that result from action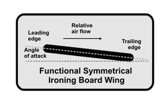 and reaction, and there certainly will not be any lift. It is only when the air flowing above the wing has a shorter transit time than that of the air flowing beneath, which is slowed due to the optimal angle of attack, that an upward lift is produced. Thus, despite the obvious element of inefficiency due to its flat and uninspiring symmetrical profile, an ordinary wing-shaped domestic ironing board mounted to the fuselage of an aircraft at an appropriate angle will generate an appreciable amount of lift.